【コンデンサの公式】

コンデンサの静電容量

：誘電率×電極板の面積／電極間の距離
　C＝ε×S／ｄ

誘電率

：比誘電率×真空誘電率
　ε＝εｒ×ε０

コンデンサの直列合成静電容量

：和分の績＝績／和
　C＝C1×C2／C1＋C2

静電エネルギー

：コンデンサの静電容量×電圧
　Q＝CV

問題
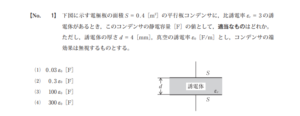
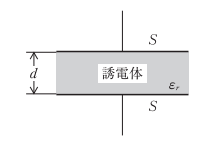
下図に示す電極板の面積Ｓ＝０．４[㎡]の平行板コンデンサに、比誘電率εｒ＝３の誘電体があるとき、このコンデンサの静電容量[Ｆ]の値として、適当なものはどれか。

ただし、誘電体の厚さｄ＝４[ｍｍ]、真空の誘電率ε０[F/M]とし、コンデンサの端効果は無視するものとする。

問題
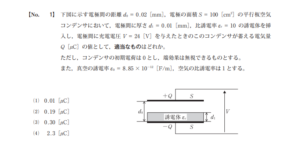
下図に示す電極間の距離ｄ０＝０．０２[ｍｍ]、電極の面積Ｓ＝１００[㎠]の平行板空気コンデンサにおいて、電極間の厚さｄ１＝０．０１[ｍｍ]、比誘電率ε１＝１０の誘電体を挿入し、電極間に充電電圧Ｖ＝２４[Ｖ]を与えたときのこのコンデンサが蓄える電気量Ｑ[μＣ]の値として、適当なものはどれか。

ただし、コンデンサの初期電荷は０とし、端効果は無視できるものとする。また、真空の誘電率ε０＝８．８５×１０の－１２条、空気の比誘電率は１とする。